2 draw root locus plot for a system with following loop transfer
Table of Contents
Table of Contents
If you’re interested in math or engineering, drawing a locus might be a skill you want to master. A locus is a set of points that meet a certain condition, and knowing how to draw one can be useful in a variety of fields. Whether you’re a student, a hobbyist or a professional, learning how to draw a locus can open up new possibilities to you.
Have you ever struggled with visualizing a solution to a math problem? Do you need to understand how a certain system behaves under different conditions? These are just a few of the pain points that can be addressed by knowing how to draw a locus. With this skill, you can more easily understand the behavior of certain systems, as well as identify solutions to complex problems.
To draw a locus, you need to identify the conditions that define the set of points you’re interested in, and then plot those points on a graph. For instance, if you want to find all the points that are equidistant from two fixed points, you would draw a circle with a radius equal to the distance between the two points. If you want to find all the points that satisfy a certain equation, you would plot the equation on a graph and identify all the points that fall on that curve.
In summary, drawing a locus requires identifying the conditions that define the set of points you’re interested in, and then plotting those points on a graph. This skill can be useful in a variety of fields, from math and engineering to physics and architecture.
How to Draw a Locus: Equidistant Points
When I was first learning how to draw a locus, I struggled with visualizing the concept. But once I understood the basic idea, I found that it was actually quite simple. One of the most common types of locus is a set of points that are equidistant from two fixed points. Here’s how you can draw this type of locus:
- First, plot the two fixed points on a graph. Label them point A and point B.
- Next, draw a circle with a radius equal to the distance between point A and point B. This will be your locus.
- Mark any point on the circle and label it point P.
- Draw line segments AP and BP.
- You should find that the lengths of AP and BP are equal, meaning that point P is equidistant from points A and B.
Here’s an image of what the locus of equidistant points would look like:
 As you can see, the locus is a circle with a center located at the midpoint between points A and B. This is because any point that is equidistant from A and B must be located on the perpendicular bisector of the line segment connecting A and B.
As you can see, the locus is a circle with a center located at the midpoint between points A and B. This is because any point that is equidistant from A and B must be located on the perpendicular bisector of the line segment connecting A and B.
How to Draw a Locus: Intersection of Lines
Another type of locus is the intersection of two lines. This type of locus can be used to find the solution to a system of linear equations. Here’s how you can draw this type of locus:
- First, plot the two lines on a graph. Label them line 1 and line 2.
- Next, find the intersection point between the two lines. This will be your locus.
- Mark the intersection point and label it point P.
Here’s an image of what the locus of intersection of lines would look like:
 As you can see, the locus is a single point, which is the intersection point between the two lines. This is because any point on both lines must satisfy both equations simultaneously, so the locus is the solution to the system of equations.
As you can see, the locus is a single point, which is the intersection point between the two lines. This is because any point on both lines must satisfy both equations simultaneously, so the locus is the solution to the system of equations.
More Complicated Loci
Of course, not all loci are as simple as the examples above. Some loci can be quite complex, especially when dealing with higher-order equations or curves.
One example of a more complicated locus is the cycloid, which is the locus of a point on the edge of a rolling circle. Drawing a cycloid requires a more advanced understanding of geometry, but the basic idea is to plot the position of a point as a circle rolls along a line. Here’s what a cycloid looks like:
 As you can see, the locus is a complex curve that is not easily described by a simple equation or geometry. Drawing a cycloid requires a lot of practice and experimentation, but it can be a rewarding challenge for anyone interested in geometry and math.
As you can see, the locus is a complex curve that is not easily described by a simple equation or geometry. Drawing a cycloid requires a lot of practice and experimentation, but it can be a rewarding challenge for anyone interested in geometry and math.
Conclusion of How to Draw a Locus
Drawing a locus can seem like a daunting task, but with a little practice and understanding, it can be a useful and rewarding skill. Whether you’re a student, a hobbyist or a professional, knowing how to draw a locus can help you solve complex problems and understand the behavior of certain systems. So why not give it a try?
Question and Answer
Q: What are some other types of loci?
A: Other types of loci include the parabola, ellipse and hyperbola. Each of these curves can be defined by different conditions, such as the set of all points that are equidistant from a fixed point and a fixed line (parabola) or the set of all points whose distances to two fixed points sum to a constant (ellipse).
Q: How can I use loci in real-life applications?
A: Loci can be used in a variety of fields, from architecture and engineering to physics and robotics. For instance, architects might use loci to find the optimal placement of windows or doors in a building, while engineers might use loci to study the behavior of a particular system under different conditions.
Q: Can I use software to draw loci?
A: Yes, there are many software programs available that can be used to draw loci. Some of the most popular include Geogebra, Desmos and Wolfram Alpha. These programs can be especially useful for drawing more complicated loci, such as the cycloid.
Q: What are some common mistakes to avoid when drawing a locus?
A: One common mistake is to confuse the locus with the set of all possible points on a graph. Remember, the locus is the set of points that meet a certain condition, so it will generally be a subset of the total set of points on the graph. Another mistake is to assume that all loci will be simple curves or shapes like circles or squares. Some loci can be quite complex, so be prepared to experiment and explore.
Gallery
Little By Little: 12.5 Drawing A Locus

Photo Credit by: bing.com / locus little draw 4cm radius asked circle points if
Locus 1
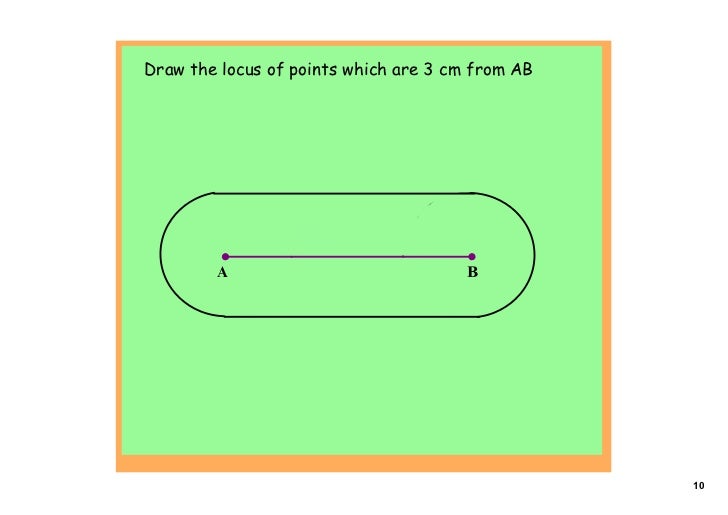
Photo Credit by: bing.com / locus
2. Draw Root Locus Plot For A System With Following Loop Transfer

Photo Credit by: bing.com / locus root loop homeworklib
Easy Steps To Draw A CYCLOID - Locus Of Point - Engg Curves - ENGG

Photo Credit by: bing.com / cycloid draw engg easy steps drawing curves locus point
How To Draw The Locus Of Point D In This Geometry Problem - Quora
Photo Credit by: bing.com / locus geometry draw problem point






